Constraint Edges – Example3

When you perform a triangulation using only the vertices of a polygon, there’s no guarantee that the resulting Delaunay triangulation will contain the original polygon’s edges. However, don’t worry; you can enforce edges in a triangulation. In the example below, we demonstrate the insertion of constraint edges into a 2D triangulation. Similarly, you can insert breaklines into 2.5D triangle meshes, as discussed in our article on Breaklines, ISO Contours and the Cookie Cutter.

Create a Delaunay triangulation

// * 1 *   Generate some input points
std::vector<Point2> vInputPoints;
vInputPoints.push_back(Point2(-100,-100));
vInputPoints.push_back(Point2(+100,+100));
vInputPoints.push_back(Point2(-50,-70));
vInputPoints.push_back(Point2(-50,-30));
vInputPoints.push_back(Point2(50,70));
vInputPoints.push_back(Point2(50,30));

// * 2 *   Triangulate the points and show
Fade_2D dt;
dt.insert(vInputPoints);
dt.show("example3_noConstraints.ps",true);

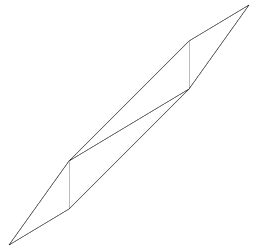
The above code creates a simple Delaunay triangulation of 6 input points but without Constraint Edges. After that, it generates the image, displayed on the right side, in Postscript format.

Insert a Constraint Edge

Next, we modify the Delaunay triangulation from the previous example. Suppose we want to create an edge from the bottom left to the top right of the triangulation. To accomplish this, we prepare one or more Segment2 objects, which we store in an std::vector. We then use this vector as an argument when calling createConstraint().

std::vector<Segment2> vSegments;
vSegments.push_back(Segment2(vInputPoints[0],vInputPoints[1]));
ConstraintGraph2* pCG;
pCG=dt.createConstraint(vSegments,CIS_CONSTRAINED_DELAUNAY);

The createConstraint() command mentioned above inserts the constraint edge without subdivision. To clarify, there are two cases in which subdivision is enforced: when the constraint edge intersects an existing vertex or when it intersects another constraint edge.

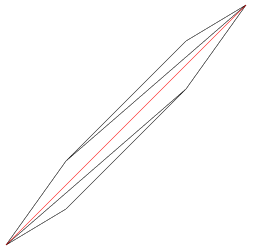
“In this example, we use CIS_CONSTRAINED_DELAUNAY as the constraint insertion strategy. You may notice that there are other strategies available; however, these are deprecated in favor of newer techniques and are kept in the API for backward compatibility.“

Subdividing Constraint Edges

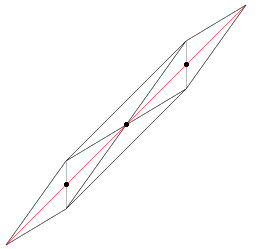
Triangles next to long Constraint Edges can have poor aspect ratios, as shown in the result image of the previous example. Subdividing the Constraint Edges results in improved adjacent triangles:

std::vector<Segment2> vSegments;
vSegments.push_back(Segment2(vInputPoints[0],vInputPoints[1]));
ConstraintGraph2* pCG;
pCG=dt.createConstraint(vSegments,CIS_CONSTRAINED_DELAUNAY);
double minLen(0.1);
pCG->makeDelaunay(minLen);

The makeDelaunay(double minLen) method in the above code facilitates this process. It recursively subdivides the constraint edges until the adjacent triangles meet the empty-circle condition. Thereby, the minLen parameter prevents excessive subdivision in narrow geometric scenarios.

Did you come across this article while looking for information on polygon triangulation? Keep going! The next article introduces the Zone concept, a valuable tool for achieving precisely that.

That covers the essentials of constraint edges. But in the domain of 2.5D, there are more options to explore. You might also find value in exploring articles like Breaklines, ISO Contours and the Cookie Cutter.

Now that you’ve become proficient in creating constraint graphs, you’re well-prepared to venture into the world of polygonal zones.