Practical Boolean Operations on Polygons with Holes – Example 6

Implementing Boolean operations on Polygons with Holes can be challenging. Therefore, in the present example, examples_2D/ex6_booleanOps2.cpp, you’ll find C++ source code already prepared to handle arbitrary shapes, whether they are convex or non-convex, with or without holes. Feel free to use this code in your project.

Additionally, it’s advisable to review the previous Example 5. This example demonstrates how to create Zone2 objects and introduces initial boolean operations using simple shapes.

The ShapeStruct

// A ShapeStruct holds its name, boundary segments and
// optionally hole segments
struct ShapeStruct
{
	ShapeStruct(const std::string& name_):name(name_)
	{}
	// Data
	std::string name; // Shape name
	vector<Segment2> vBoundarySegments; // Shape boundary
	vector<vector<Segment2> > vvHoles; // vectors of segments for n holes
};

The above struct ShapeStruct holds one vector of boundary segments that describe the outer boundary of a shape and a vector of vector<Segment2> that describes holes in this shape.

You may have noticed the presence of GASSEX() statements in the examples. The GASSEX macro serves as a more flexible alternative to assert() and can be found in “someTools.h”. Its use is optional, but it is strongly recommended to use GASSEX frequently in your code for two primary purposes: First, to automatically detect unexpected runtime conditions, and second, to enhance the verbosity of your code.

The main() function

// * 1 *   Create 3 random ShapeStructs
const int NUMHOLES(2);
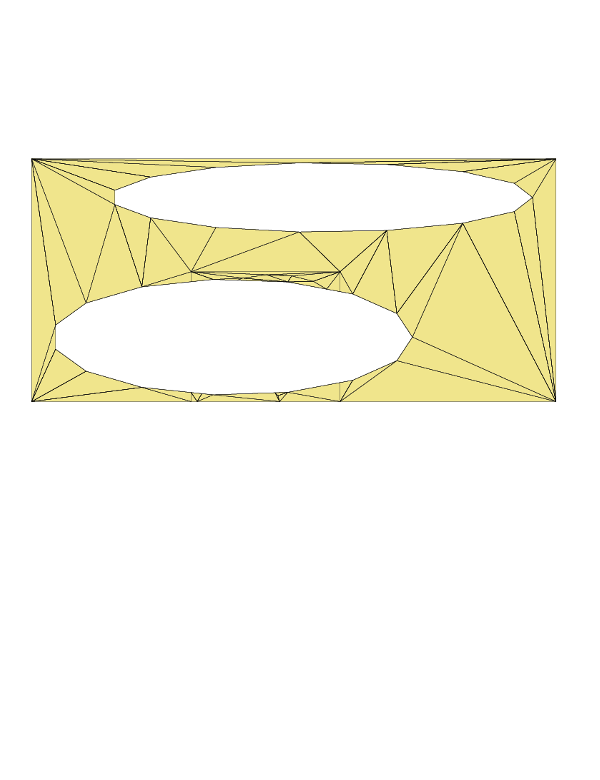
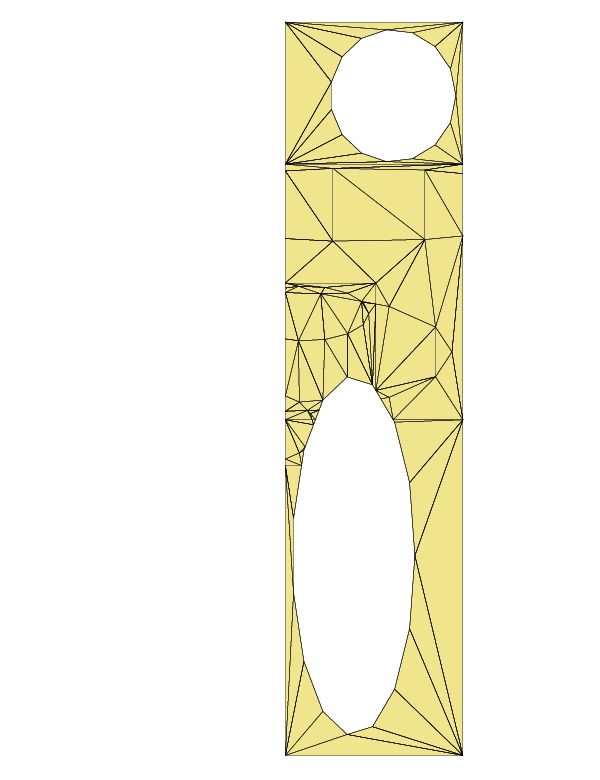
vector<ShapeStruct> vShapes({	ShapeStruct("Alpha"),
								ShapeStruct("Beta"),
								ShapeStruct("Gamma")});
for(size_t i=0;i<vShapes.size();++i)
{
	createShape(vShapes[i],NUMHOLES);
}

// * 2 *   Convert the ShapeStructs to Zones 
Fade_2D dt;
vector<Zone2*> vZones;
for(size_t i=0;i<vShapes.size();++i)
{
	ShapeStruct& shape(vShapes[i]);
	Zone2* pZone=insertZone(dt,shape);
	GASSEX(pZone!=NULL);
	vZones.push_back(pZone);
	pZone->show(("example6_zone"+shape.name+".ps").c_str(),false,false);
}

dt.show("example6_constrainedDelaunay.ps");

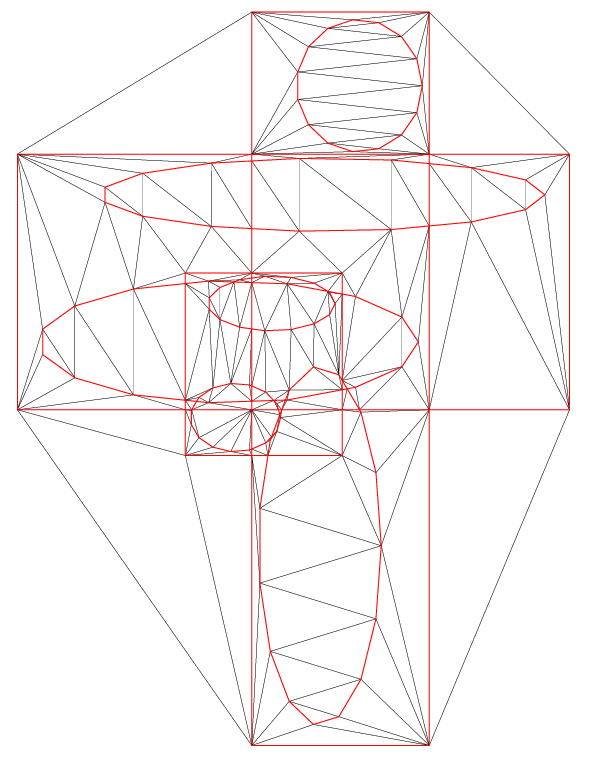
// * 3 *   Boolean union operation
Zone2* pResultZone(vZones[0]);
for(size_t i=1;i<vZones.size();++i) pResultZone=zoneUnion(pResultZone,vZones[i]);

// * 4 *   Visualize the result
pResultZone->show("example6_union.ps",false,true);
vector<Triangle2*> vTriangles;
pResultZone->getTriangles(vTriangles);
cout<<"pResultZone, Number of triangles: "<<vTriangles.size()<<endl;
cout<<"pResultZone, 2D-area: "<<pResultZone->getArea2D()<<endl;

return 0;

• In Step 1 of the listing above, the createShape() function is invoked to generate three random polygons with holes. These polygons are stored as ShapeStructs. There’s no need to delve into the details of the createShape() function because it simply acts as a placeholder for your actual polygon data.
• Moving on to Step 2, the insertZone() function is used to transform each ShapeStruct into a Zone2 object.Next, Step 2 uses insertZone() to turn each ShapeStruct into a Zone2 object.
• The third step computes the union of the zones.
• Finally, in Step 4, the result is drawn and printed:

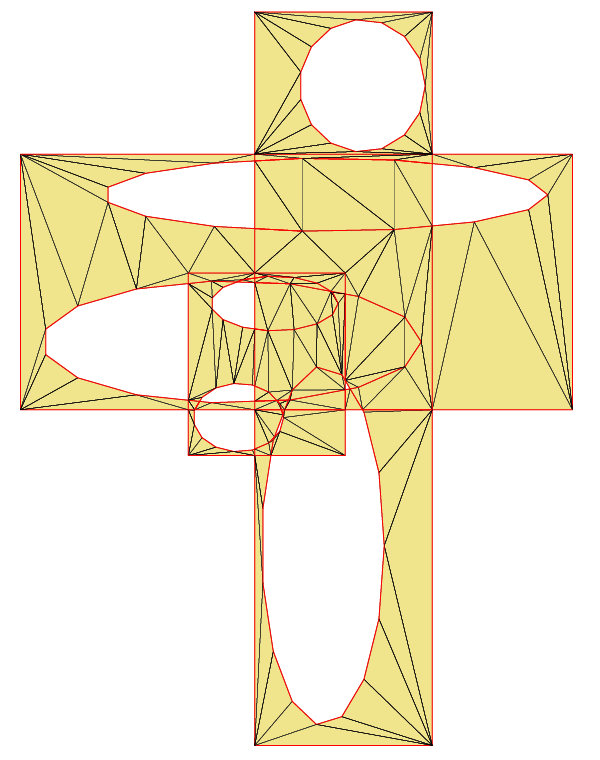
Visualizer2:: Writing example6_union.ps

pResultZone, Number of triangles: 195

pResultZone, 2D-area: 2083.77

The insertZone() function

The Shapestruct defined above is only a collection of line segments. Therefore, insertZone() becomes particularly relevant as it takes these segments, inserts them into a Delaunay triangulation, transforms them into a Zone2, and then returns a pointer to it.

Zone2* insertZone(Fade_2D& dt,ShapeStruct& shape)
{
	// Create the boundary zone
	ConstraintGraph2* pBoundaryCG=\
      dt.createConstraint(shape.vBoundarySegments,CIS_CONSTRAINED_DELAUNAY);
	Zone2* pZone(dt.createZone(pBoundaryCG,ZL_INSIDE));
	
	// Create and subtract the holes (if any)
	for(vector<Segment2>& vHole : shape.vvHoles)
	{
		if(vHole.empty()) continue; // Unusable
		ConstraintGraph2* pHoleCG=\
          dt.createConstraint(vHole,CIS_CONSTRAINED_DELAUNAY);
		Zone2* pHoleZone(dt.createZone(pHoleCG,ZL_INSIDE));
		pZone=zoneDifference(pZone,pHoleZone);
	}
	return pZone;
}