This example shows how to generate a fast Voronoi diagram in C++. A Voronoi diagram (Wikipedia) divides the plane into convex regions around a set of input points, so that each region contains all locations closest to one particular point. Voronoi diagrams appear in many areas of science and engineering, from physics and biology to computer graphics and spatial analysis.
A good Voronoi library should provide fast point-location queries, be robust against degenerate cases, and handle infinite cells to be practical and easy to use. Fade2D meets these properties. In this tutorial, we’ll explore a C++ example you can also find in ‘examples_2D/ex12_voronoi.cpp‘.
A Voronoi diagram in C++
The code below creates a few points and inserts them into a Delaunay triangulation. Then it retrieves its dual graph, which is the Voronoi diagram:
std::cout<<"* Example12: Voronoi - Point location in a Voronoi diagram"<<std::endl;
// * Step 1 * Create input points (on circles and on a grid). Each
// of these plays two roles: It is a Delaunay-Vertex
// AND a site of one Voronoi cell.
std::vector<Point2> vPoints;
generateCircle( 20,25,75,20,20,vPoints);
generateCircle( 10,25,75,10,10,vPoints);
generateCircle( 20,75,35,10,30,vPoints);
for(double x=0;x<41.0;x+=10)
{
for(double y=0.0;y<41;y+=10)
{
vPoints.push_back(Point2(x+.5,y+.5));
}
}
// * Step 2 * Draw the Voronoi diagram and Delaunay triangulation
// Infinite Voronoi cells are automatically clipped.
Fade_2D dt;
dt.insert(vPoints);
Voronoi2* pVoro(dt.getVoronoiDiagram());
pVoro->show("voronoi_and_delaunay.ps",true,false,true,true,false); // Options: Voro=true,Fill-Colors=false,Sites=true,Delaunay=true,Labels=false
pVoro->show("voronoi_and_sites.ps",true,true,true,false,false); // Options: Voro=true,Fill-Colors=true,Sites=true,Delaunay=false,Labels=false
...- Step 1 creates a set of input points, some lying on a circle, and others arranged on a grid.
- Step 2 triangulates the input, then obtains the Voronoi diagram using
Fade_2D::getVoronoiDiagram(), and finally generates two visualizations. That’s it, see the resulting images below.
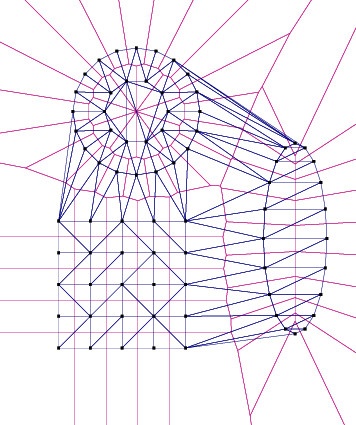
Hint: If you prefer working only with finite Voronoi cells, here’s a simple trick: compute the bounding box of your sites, enlarge it by a factor of 10, and then add its four corner points to the sites. This makes all previously infinite cells finite.
Nearest neighbor search / cell search
The code snippet below finds the Voronoi cell containing an arbitrary query point. It then generates another visualization.
// * Step 3 * Assign arbitrary indices to the Voronoi cells. This
// is completely optional. You can use this feature
// for visualization OR to associate Voronoi cells with
// your own data structures.
std::vector<VoroCell2*> vVoronoiCells;
pVoro->getVoronoiCells(vVoronoiCells);
for(size_t i=0;i<vVoronoiCells.size();++i)
{
VoroCell2* pVoro(vVoronoiCells[i]);
pVoro->setCustomCellIndex(int(i));
}
// * Step 4 * Locate the cell of an arbitrary query point.
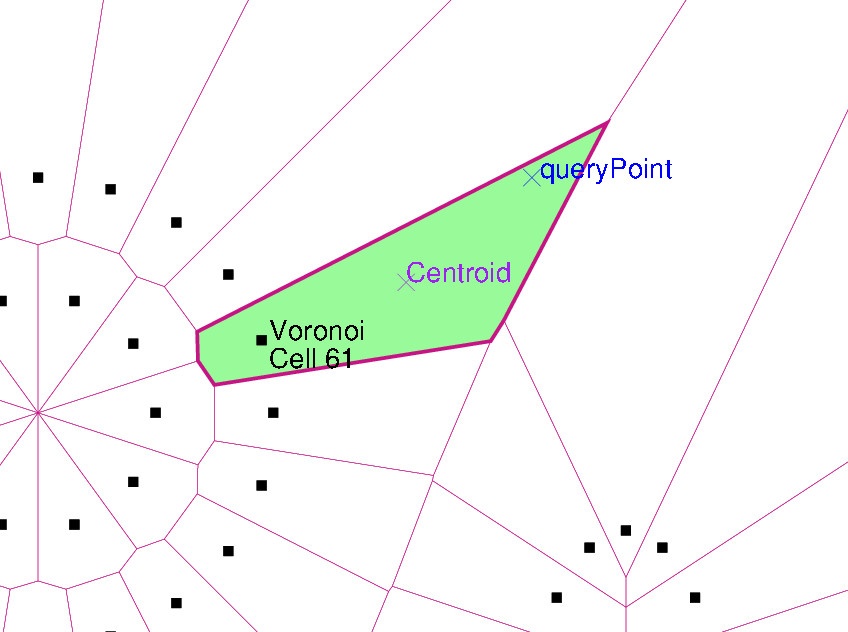
Point2 queryPoint(67,95);
VoroCell2* pVoroCell(pVoro->locateVoronoiCell(queryPoint));
Visualizer2 v("located_cell.ps");
Bbox2 bbx(dt.computeBoundingBox());
bbx.enlargeRanges(1.5);
v.setLimit(bbx); // Manually set a limit to clip the viewport.
pVoro->show(&v,true,false,true,false,false); // Options: Voro=true,Fill-Colors=false,Sites=true,Delaunay=false,Labels=false
v.addObject(Label(queryPoint," queryPoint"),Color(CBLUE));
if(pVoroCell!=NULL)
{
int cellIdx(pVoroCell->getCustomCellIndex());
std::cout<<"Found the voronoi cell no. "<<cellIdx<<std::endl;
// Color the located cell red
v.addObject(pVoroCell,Color(CPALEGREEN,1.0,true));
// Write a label that shows its custom cell-index
Label l(*pVoroCell->getSite(),
(" Voronoi\n Cell "+toString(cellIdx)).c_str(),false);
v.addObject(l,Color(CBLACK));
Point2 centroid;
double area=pVoroCell->getCentroid(centroid);
if(area<0)
{
std::cout<<"Cell "<<cellIdx<<" is infinite: No area, no centroid"<<std::endl;
}
else
{
std::cout<<"Cell "<<cellIdx<<": area="<<area<<", centroid="<<centroid<<std::endl;
v.addObject(Label(centroid,"Centroid"),Color(CPURPLE));
}
v.writeFile();
}
- Step 3 is optional: it fetches all Voronoi cells and assigns each an arbitrary integer index. This is useful for relating the cells to your own data structures, and you can use these indices as labels for a visualization.
- The first two lines in Step 4 locate the Voronoi cell of the query point (x=67.0, y=95.0). The remaining lines draw the diagram with this cell highlighted, and mark the
site, itscentroid, and thequeryPoint.
Observe that only finite cells have a centroid and a finite area. Fade returns
-1for the area of infinite cells.
Note: The Voronoi diagram is the dual graph of the Delaunay triangulation, but NOT of a constrained Delaunay triangulation. If your triangulation contains constraint edges, make them conforming using
ConstraintGraph2::makeDelaunay()before accessing the Voronoi diagram.”
Point location benchmark
The 2D Delaunay Triangulation Benchmark shows that Delaunay triangulations are very fast. Due to their duality, constructing Voronoi diagrams is equally efficient. However, we must also benchmark nearest neighbor queries (i.e., quickly locating cells) as shown in the code below.
// * Step 5 * Benchmark mass point location (typ. 0.2 s for 1 mio queries)
std::vector<Point2> vRandomPoints;
generateRandomPoints(1000,0,100,vRandomPoints,1);
Fade_2D dt2;
dt2.insert(vRandomPoints);
Voronoi2* pVoro2(dt2.getVoronoiDiagram());
pVoro2->show("mass_location.ps",true,true,false,false,false); // Options: Voro=true,Fill-Colors=true,Sites=false,Delaunay=false,Labels=false
timer("massLocate");
for(int i=0;i<1000000;++i)
{
double x(100.0 * double(rand())/RAND_MAX);
double y(100.0 * double(rand())/RAND_MAX);
Point2 q(x,y);
VoroCell2* pVoroCell(pVoro2->locateVoronoiCell(q));
unusedValue(pVoroCell); // Avoids an unused-warning
}
timer("massLocate");
return 0;- Step 5 triangulates 1,000 points, then retrieves the dual graph
pVoro2. Then it enters the"massLocate"timer-section, where it finds the containing Voronoi cell for 1 million random query points . This takes only about 0.3 seconds, with time consumption growing only logarithmically with the number of cells.
Feel free to link to this site if you find it useful and want to support it!
