Welcome to our guide to Delaunay triangulation with C++. In this article, we’ll introduce you to the Fade2D library and show you how to perform a basic Delaunay triangulation on four points. This article serves as both an overview of the library and a practical example to get you started. Fade2D is a powerful library…Continue readingC++ Examples for Delaunay Triangulation – Getting Started (0)
Author: Bernhard Kornberger
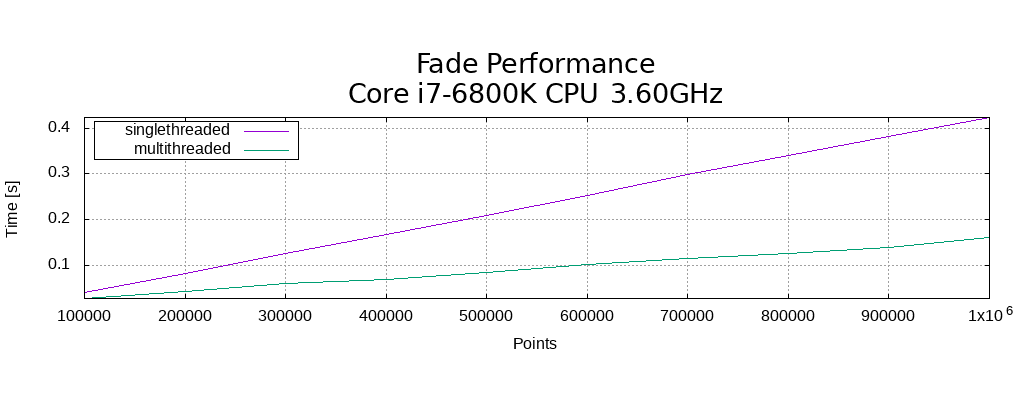
Fade2D is a powerful C++ Delaunay triangulation library known for its speed and robustness. In this benchmark, we explore its performance in triangulating varying point cloud sizes. Performance and Settings Benchmark Code Benchmarking Single- and Multithreaded Delaunay Triangulation In this section, we take a closer look at benchmarking Fade2D’s performance, both in single-threaded and multithreaded…Continue reading2D Delaunay Triangulation Benchmark – Example1
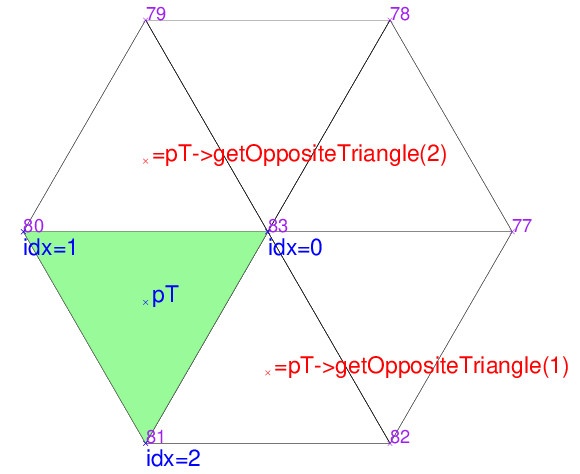
In this article, we will achieve two main objectives: first, we’ll explore how to access the elements within a triangulation, and second, we’ll demonstrate how to draw them in Postscript format. This visualization is crucial as it enables you to visualize your source code’s outcomes. Preparing a triangulation Let’s start by preparing and drawing a…Continue readingAccessing Triangulation Elements and Drawing Postscript – Example2
When you perform a triangulation using only the vertices of a polygon, there’s no guarantee that the resulting Delaunay triangulation will contain the original polygon’s edges. However, don’t worry; you can enforce edges in a triangulation. In the example below, we demonstrate the insertion of constraint edges into a 2D triangulation. Similarly, you can insert…Continue readingConstraint Edges – Example3
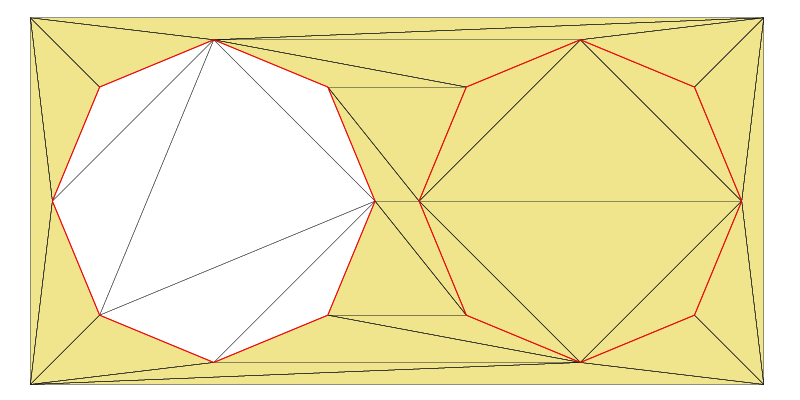
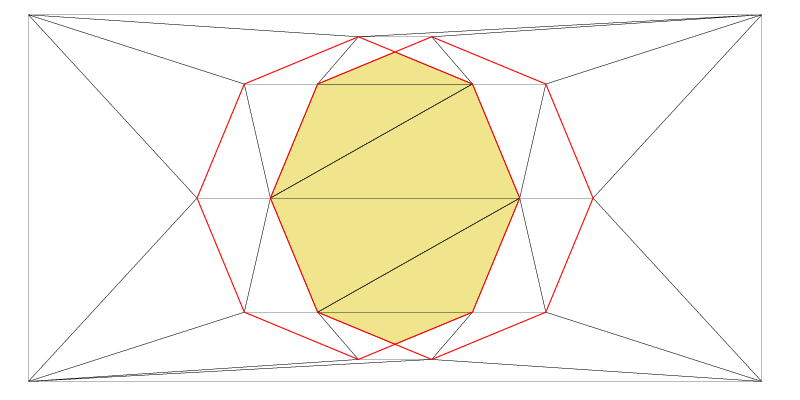
If you want to perform polygon triangulation or work with polygon clipping, you’re in the right place. In Fade, a Zone2 object defines a specific area within a triangulation. You can define a zone in the following ways: It allows you to combine shapes using the Boolean set operations union, difference, symmetric difference, and intersection.…Continue readingPolygons and Zones – Example4
Polygon Clipping, Boolean Set Operations Fade provides polygon clipping and functions to combine shapes through the boolean operations: You can find the C++ source code for the polygon clipping demo in examples_2D/ex5_booleanOps.cpp in the Fade download. Creating two Shapes “This demo code creates two input shapes using code similar to what was shown in Polygons…Continue readingPolygon Clipping, Boolean Operations – Example5
Implementing Boolean operations on Polygons with Holes can be challenging. Therefore, in the present example, examples_2D/ex6_booleanOps2.cpp, you’ll find C++ source code already prepared to handle arbitrary shapes, whether they are convex or non-convex, with or without holes. Feel free to use this code in your project. Additionally, it’s advisable to review the previous Example 5.…Continue readingPractical Boolean Operations on Polygons with Holes – Example 6
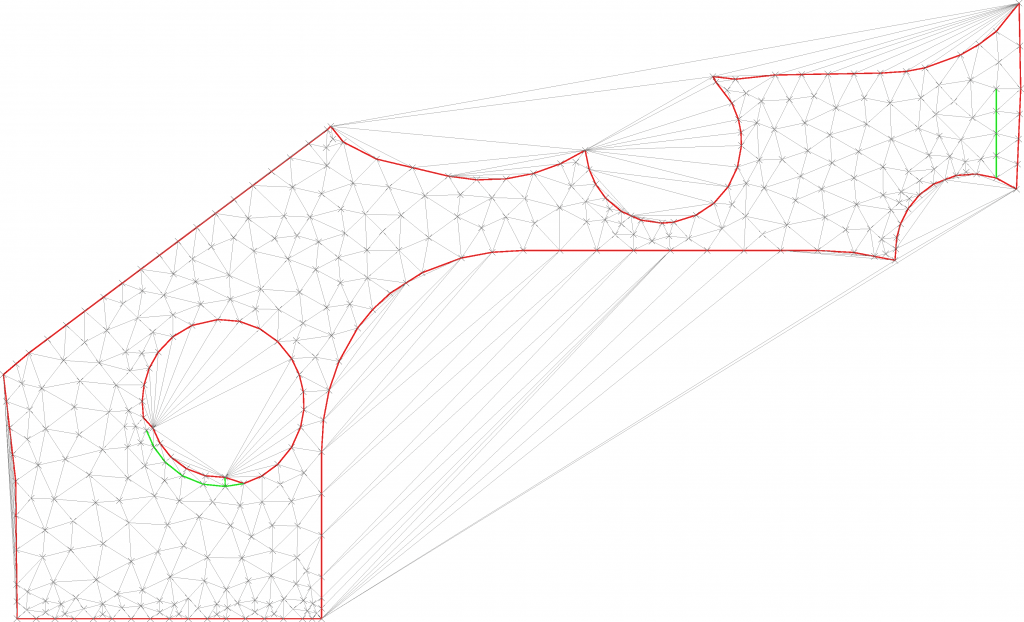
Delaunay meshing is not merely about creating a mesh on points; it’s about Quality Meshing. This involves crafting a Delaunay mesh with triangles that meet certain quality criteria, such as minimal interior angles or maximum edge lengths. These properties are typically achieved by adding points, effectively refining an existing triangulation. You can find the source…Continue readingAdvanced Delaunay Meshing – Example 7
A frequently asked question is how to export a triangulation as a list of points and indices for use in one’s own software. Users have two options: they can implement this themselves using custom indices, or they can utilize the FadeExport data structure. Using FadeExport is more memory-efficient as it releases memory within Fade while…Continue readingExporting a Triangulation – Example 8
When coding geometry software, numerical errors and unexpected geometric settings occur frequently. Thus, automated software testing with random geometric data is essential. But, for instance, creating random polygons without self-intersection is not trivial. Therefore the module testDataGenerators is provided to create repeatable sequences of random geometric objects for software testing and debugging. These include random…Continue readingRandom Polygons, Surfaces and more – Example 9
Fade2D is fast, and most of the time, you will not need progress updates at all. However, for very large triangulations, you may still want to connect your own progress bar to Fade2D’s update mechanism. Creating Your Custom Progress Receiver Class To receive progress information, you must create a custom class in your software that…Continue readingProgress Bar Mechanism – Example 10
Manually saving and loading a triangulation is challenging. This is especially true when there are millions of elements, and speed is crucial. For this reason, there are functions in Fade2D to assist you in saving and loading a triangulation, its zones and constraint edges. The included file “examples_2D/ex11_save_and_load.cpp” provides simple demo source code for this…Continue readingSaving and Loading a Triangulation – Example 11
This is a fast C++ Voronoi diagram example. The Voronoi diagram (Wikipedia) divides the plane into convex regions around the input points such that each region is closest to one point. There is an incredible number of applications for the Voronoi diagram so many scientists and engineers are familiar with this basic concept. A C++…Continue readingVoronoi Diagram 2D in C++, Example 12
2.5D Delaunay triangulations (TIN – Triangulated Irregular Networks) are like a 2D Delaunay triangulation, but with elevated points. This article first describes the simple triangulation of point clouds from LiDAR scans and surface metrology data. It then demonstrates their optional simplification using adaptive and grid-based clustering methods. Finally, it shows how to re-export the triangle-mesh…Continue reading2.5D Terrain Triangulation and Point Cloud Simplification
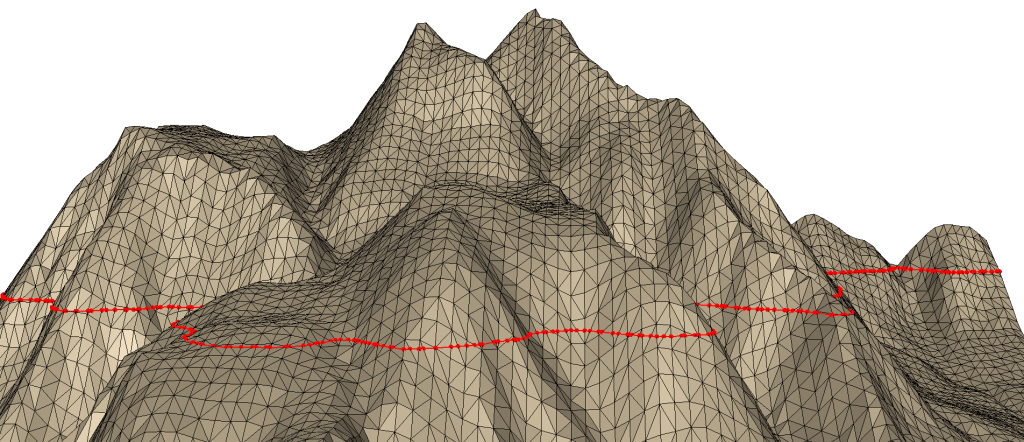
In this example, we will flip edges in an unnatural looking triangulation to better match its valleys and ridges. Further we will use Fade’s Weighted Laplacian smoothing technique to improve the quality of a noisy triangle mesh. And finally we address an annoying problem, namely large edges at the boundary of a triangulation and we…Continue readingValleys and Ridges, Smoothing, Mesh-Improvements
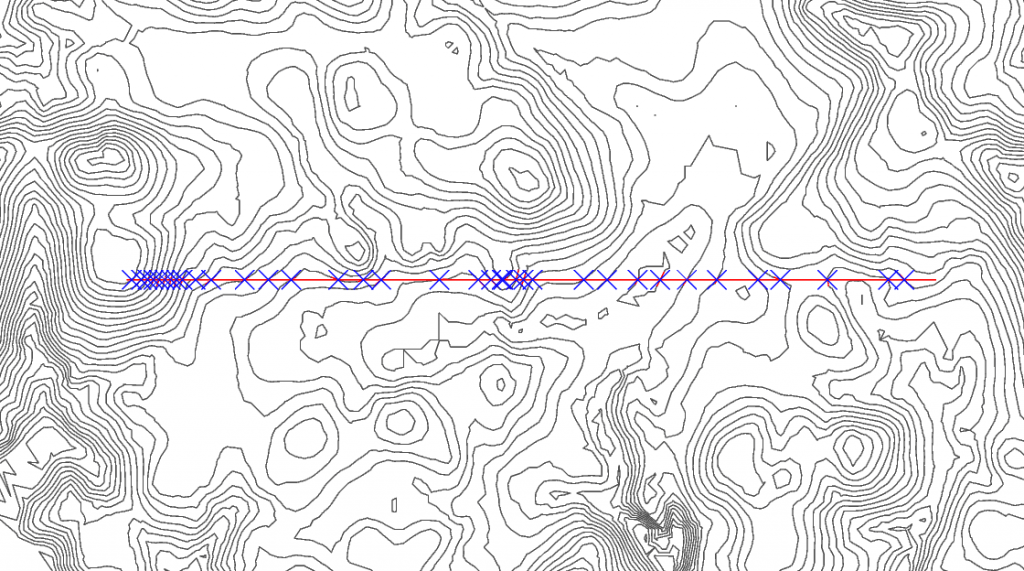
In the field of land surveying constraint edges are maybe better known as “breaklines”. Similarly to the 2D case you can insert them into the triangle mesh, forcing segment subdivision or not. In addition you can insert a segment with its original height or you can adjust its height to the triangulation. This results in…Continue readingBreaklines, ISO Contours and the Cookie Cutter
The Segment Checker computes intersections of 2D or 2.5D line segments. But in contrast to 3D two line segments are considered to intersect when their 2D projections in the xy-plane intersect. In other words, even if the involved segments are at different heights. The Segment Checker is fast and robust against degenerate and glancing intersections.…Continue readingSegment Checker for 2D and 2.5D Segment Intersections
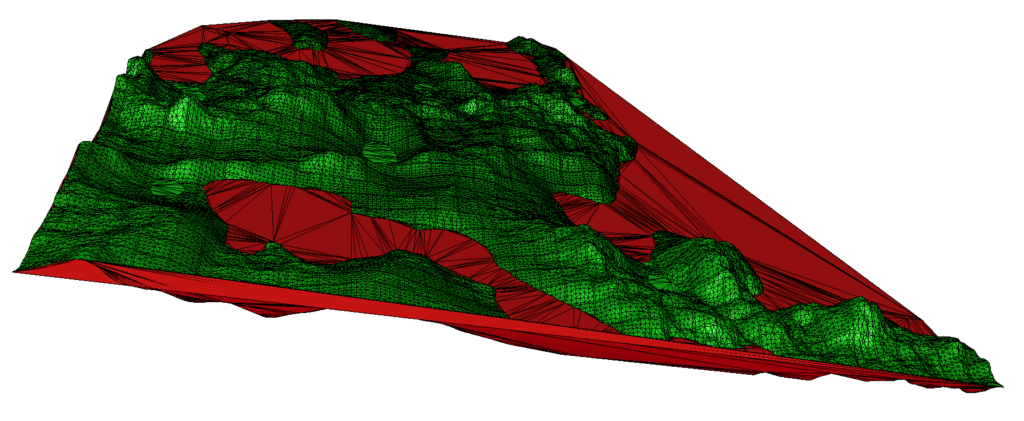
If you’re a software developer in land surveying, you understand the importance of processing large point clouds efficiently. You also know the critical role of triangle filtering to generate correct terrain representations. Automatically removing unwanted triangles while retaining the important ones is a crucial step in achieving this goal. In this article, we’ll explore a…Continue readingTriangle Filtering: A Practical Solution in Land Survey Software
Cut And Fill (Wikipedia) Earthwork volume computations for C++. The library module Cut-And-Fill takes two overlapping surfaces and computes the volume between. The result is a set of volumes where soil must be filled or where material must be digged off to turn one surface into the other one. Example Source Code – Basic Usage…Continue readingCut and Fill Volumes in C++