Categories
Fade2.5D Examples

Breaklines, ISO Contours and the Cookie Cutter

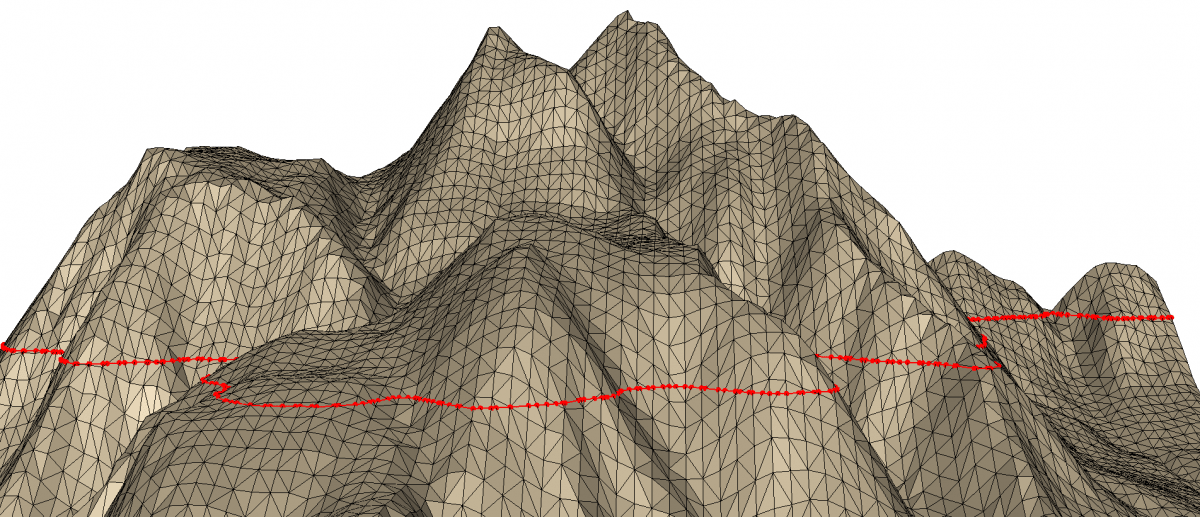
ISO Contours computed from the test terrain
ISO-Contours and Breaklines

In the field of land surveying constraint edges are maybe better known as “breaklines”. Similarly to the 2D case you can insert them into the triangle mesh, forcing segment subdivision or not. In addition you can insert a segment with its original height or you can adjust its height to the triangulation. This results in the four possibilities:

  1. A breakline is inserted at its original elevation
  2. It is inserted at its original elevation and subdivided
  3. A breakline is projected to the surface and then it is inserted
  4. Or it is projected to the surface, then it is subdivided and inserted (this is most likely what you want)

Breakline insertion at breakline elevation

The first two methods pose the simplest case because they just insert the breaklines at their own elevation:

// 2: Insert breaklines (with subdivision, no drape)
void terrain_breaklines_withSubdiv_noDraping()
{
	// * 1 *   Create a surface and some segments
	Fade_2D dt;
	createTriangulation(dt);
    vector<Segment2> vSegments;
    createCircularPolygon(vSegments);

	// * 2 *   Insert the segments ('breaklines')
    bool bOrientedSegments(false); // Not required for this demo
    bool bUseHeightOfLatest(true); // When a constraint crosses an existing one, the split point gets z from the last inserted constraint if true
    ConstraintGraph2* pCG=dt.createConstraint(vSegments,CIS_CONSTRAINED_DELAUNAY,bOrientedSegments,bUseHeightOfLatest);
    double minLen(0.1);
    pCG->makeDelaunay(minLen); // Subdivision

	// * 3 *   Visualize
	Visualizer3 vis("c2_terrain_withSubdiv_noDraping.list"); // For the Geomview viewer (Linux)
	dt.showGeomview(&vis,Visualizer3::CWHEAT);
	vis.writeSegments(vSegments,"0 0 1 0.5",true);
	dt.show("c2_terrain_withSubdiv_noDraping.ps"); // Postscript for gv, gsview or online ps-viewers
}
  1. Step 1 creates a triangulation and a vector of line segments.
  2. Then the second step calls Fade_2D::createConstraint() to insert the segments as breaklines. Optionally makeDelaunay() can be called to subdivide the segments.

“The makeDelaunay() method subdivides line segments until all sub-edges satisfy the empty cirlce property. This property is probably more useful in combination with breakline-insertion at surface elevation further below.”

Breakline insertion without subdivision, without draping
Breakline insertion without subdivision, without draping
Breakline insertion with subdivision, without draping
Breakline insertion with subdivision, without draping

“Any point(x,y) has exactly one height z. When you insert a breakline that conflicts with existing vertices or breaklines then the height of existing elements has higher priority. However, you can change this behavior using bUseHeightOfLatest=true like shown in the above source code.

Breaklines at surface elevation

We want to insert breaklines (blue) at surface elevation (red). For this purpose we need one preparatory function call: We drape the segments (blue) onto the surface (red).

Breakline insertion without subdivision, with draping
Breakline insertion without subdivision, with draping
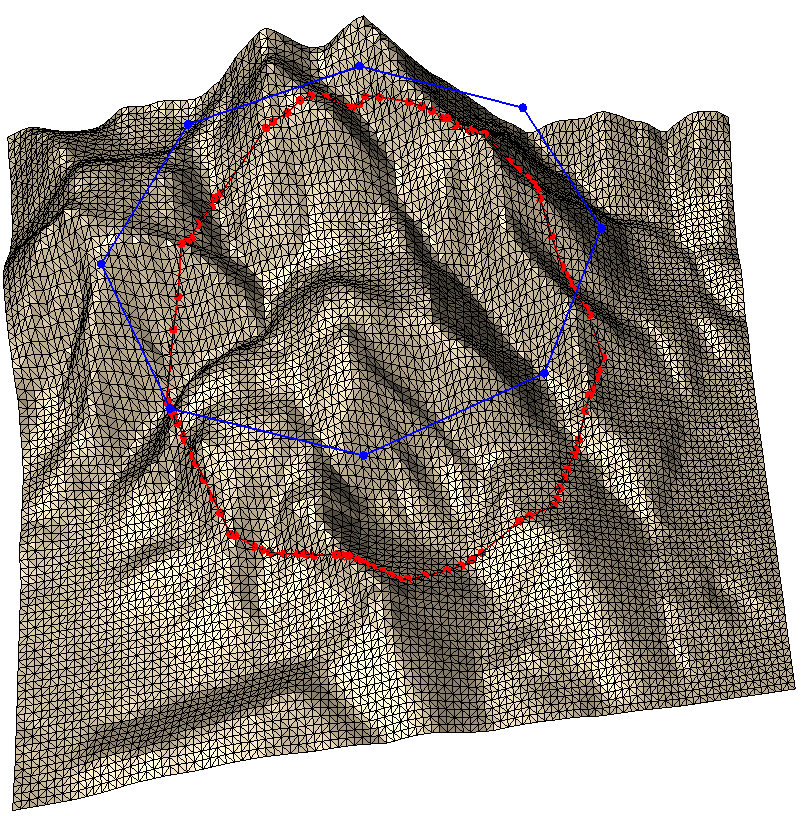
Breakline insertion with subdivision, with draping
Breakline insertion with subdivision, with draping. This is the most common method.
// 3: Insert breaklines (with subdivision, with drape)
void terrain_breaklines_withSubdiv_withDraping()
{
    ...
    // * 2 *   Insert the segments ('breaklines')
	double zTolerance(.1);
	vector<Segment2> vDrapedSegments;
	dt.drape(vSegments,vDrapedSegments,zTolerance);
	ConstraintGraph2* pCG=dt.createConstraint(vDrapedSegments,CIS_CONSTRAINED_DELAUNAY);
	double minLen(0.1);
	pCG->makeDelaunay(minLen); // Subdivision
    ...
}

In the above code Fade_2D::drape() drapes the original segments onto the triangulation. But this could require a large number of subdivisions. For this reason we use zTolerance>0 to reduce the number of subdivisions i.e., to subdivide a segment only if required to keep this distance to the surface. In contrast we could also use zTolerance=-1 to split the original segments at all intersections with triangulation edges. Finally we insert the draped segments into the TIN using Fade_2D::createConstraint() as before.

An often required function is the cutting of triangle meshes. You can do this with the above described breaklines, but for convenience a separate function is available, with which you can easily cut out parts of a mesh like with a cookie cutter. Have a look at the below code snippet:

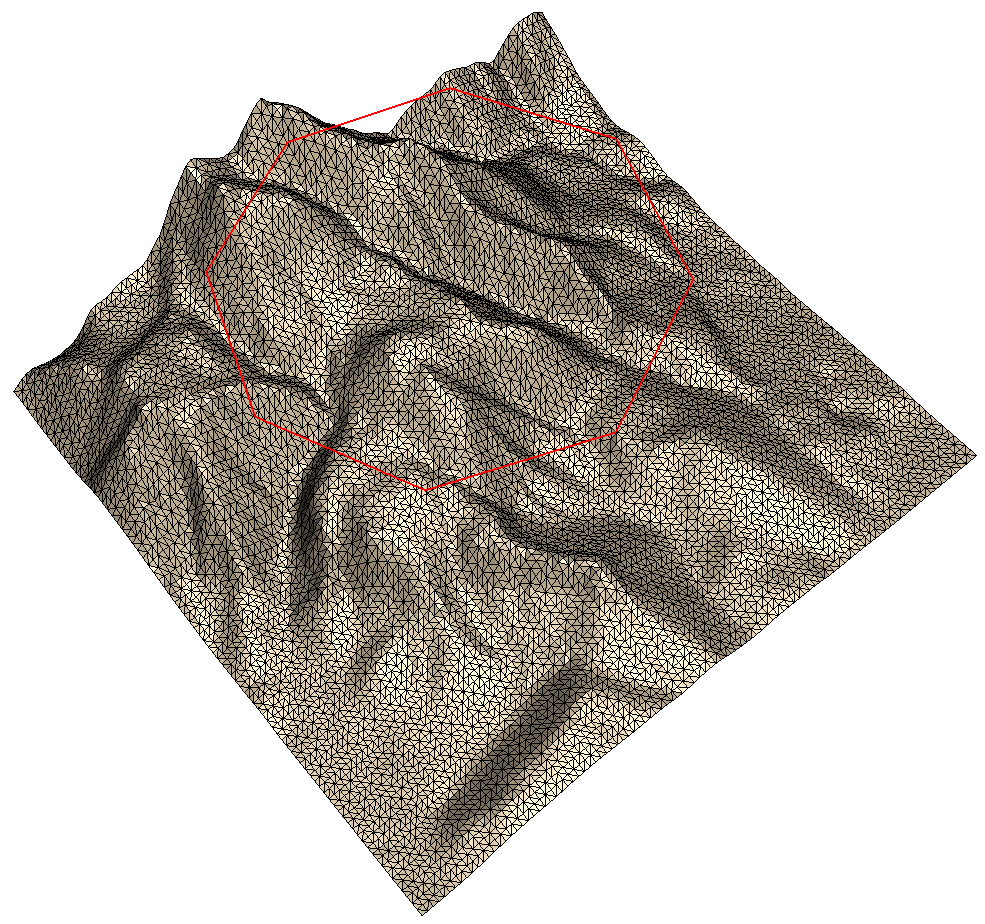
Terrain with polygonal knife segments (cookie cutter)
Terrain with polygonal knife segments in red (cookie cutter)
The cut out terrain piece (the cookie)
The cut out terrain piece (cookie)
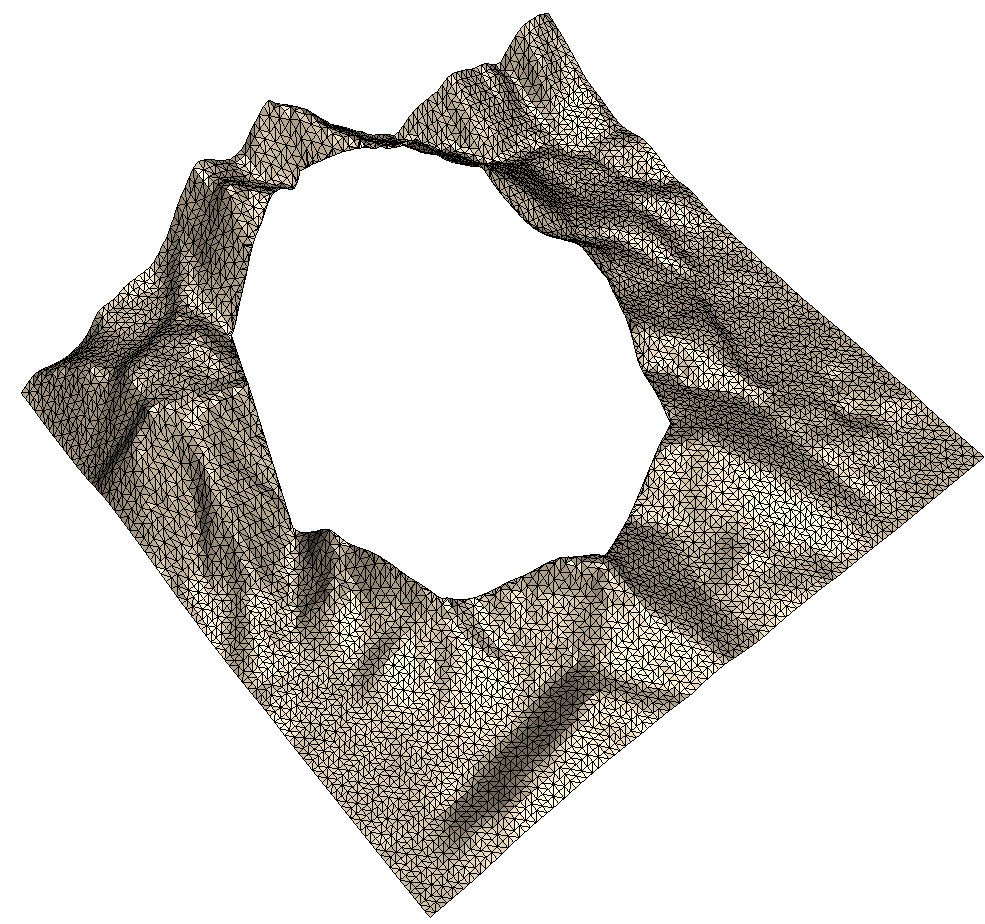
Terrain, complementary set of triangles
Terrain, complementary set of triangles
// 4: Cookie Cutter
void cookieCutter()
{
	// * 1 *   Create a surface and a polygon
	Fade_2D dt;
	createTriangulation(dt);
    vector<Segment2> vPolygon;
    createCircularPolygon(vPolygon);

	// * 2 *   Show the triangulation and the polygon
	Visualizer3 vis("c4_surface.list");
	Zone2* pGlobalZone(dt.createZone(NULL,ZL_GLOBAL));
	pGlobalZone->showGeomview(&vis,Visualizer3::CWHEAT);
	vis.writeSegments(vPolygon,Visualizer3::CRED);

	// * 3 *   Cut out a piece with the cookieCutter
	Zone2* pCookie(dt.createZone_cookieCutter(vPolygon,true));
    pCookie->showGeomview("c4_cookie.list",Visualizer3::CGREEN);

	// * 4 *   Compute also the complementary piece
	Zone2* pNotCookie(zoneDifference(pGlobalZone,pCookie));
	pNotCookie->showGeomview("c4_notCookie.list",Visualizer3::CWHEAT);
  
    // * 5 *   Save the triangulation and the zones to a file
    vector<Zone2*> vSaveZones;
    vSaveZones.push_back(pCookie);
    vSaveZones.push_back(pNotCookie);
    bool bSaveOK(false);
    std::ofstream file("c4_triangulation.fade",std::ios::binary);
    if(file.is_open())
    {
        // Use a filename or std::ostream as first argument
        bSaveOK=dt.saveTriangulation(file,vSaveZones);
        file.close();
    }
    if(!bSaveOK)
    {
        cout<<"File not written"<<endl;
        return;
    }

    // * 6 *   Load the triangulation from the file
    Fade_2D dt2;
    vector<Zone2*> vLoadZones;
    bool bLoadOK=dt2.load("c4_triangulation.fade",vLoadZones); // istream works also
    if(!bLoadOK)
    {
        cout<<"File not loaded"<<endl;
        return;
    }
    for(size_t i=0;i<vLoadZones.size();++i)
    {
        Zone2* pZone(vLoadZones[i]);
        string name("c4_reloadZone_"+toString(i)+".ps");
        pZone->show(name.c_str(),true,false);
    }

}
  1. Step 1 creates a triangulation (the stored mountain). Then it creates a circular polygon consisting of a few Segment2 objects
  2. The second step creates a Zone2* pGlobalZone consisting of all triangles. Then it visualizes this zone along with the segments from Step 1.
  3. The third step creates the zone pCookie using the polygon as parameter for the method createZone_cookieCutter().
  4. Step 4 uses the boolean operation zoneDifference() to create also a zone pNotCookie consisting of the complementary set of triangles. You might review Polygon Clipping, Boolean Operations – Example5.
  5. Step 5 saves the triangulation and the two zones pCookie and pNotCookie using Fade_2D::saveTriangulation(). You may refer to Saving and Loading a Triangulation for details.
  6. Finally Step 6 reloads the stored triangulation using Fade_2D::load() and it draws the two zones.

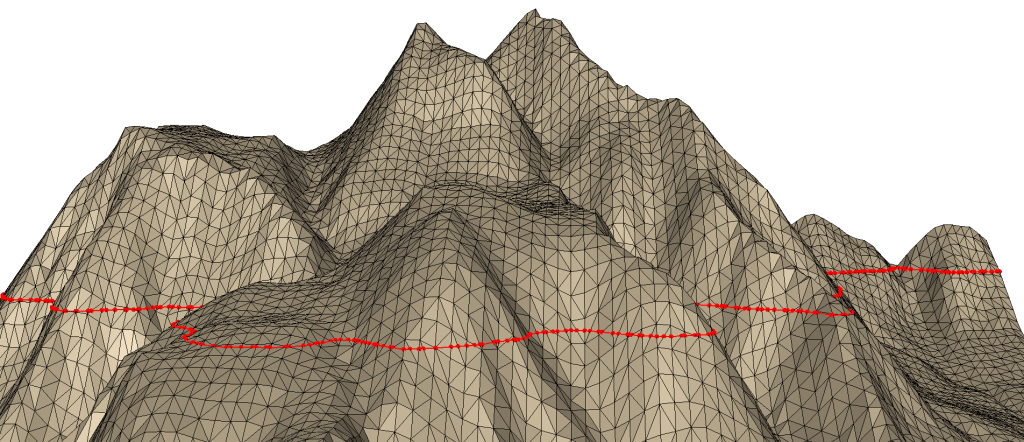
ISO contour computation

ISO Lines from a large terrain at different elevations
Terrain triangulation 2.5D, ISO contours of 550 000 triangles at 30 different levels computed in 0.38 seconds.

Iso contours are lines consisting of the intersection of a terrain with a horizontal plane at a certain height i.e., at a certain z-value. Fade has an exceptionally fast algorithm to calculate iso lines. We use it like this:

  1. Create a triangulation and fetch the triangles in vTriangles
  2. Create IsoContours icoc(vTriangles)
  3. Call isoc.getContours(), the parameters are the query-height as well as a vector of vector<Segment2> which is used to return the polylines.
// 5: Compute ISO lines (intersection with a horizontal plane)
void isoContours()
{
	// * 1 *   Create a surface and fetch the triangles
	Fade_2D dt;
	createTriangulation(dt);
	std::vector<Triangle2*> vTriangles;
	dt.getTrianglePointers(vTriangles);

    // * 2 *   Create IsoContours isoc
    IsoContours isoc(vTriangles);
    double minZ(isoc.getMinHeight());
    double maxZ(isoc.getMaxHeight());
    double height(minZ+0.45*(maxZ-minZ));

	// * 3 *   Compute the contours
	std::vector<std::vector<Segment2> > vvContours;
	isoc.getContours(height,vvContours,true,true);
	cout<<vvContours.size()<<"polylines at height "<<height<<endl;

    // Write the result
	for(size_t i=0;i<vvContours.size();++i)
	{
		std::vector<Segment2>& vContour(vvContours[i]);
		cout<<"\nContour no. "<<i<<" consists of "<<vContour.size()<<" segments"<<std::endl;
		vis.writeSegments(vContour,"1 0 0 0.5",true);
		for(size_t i=0;i<vContour.size();++i)
		{
			cout<<vContour[i]<<endl;
		}
    }
}
ISO Contours computed from the test terrain
ISO Contours computed from the mountain test model

Height queries

Fade2.5D supports fast 2.5D height queries with arbitrary (x,y) coordinate pairs. The method bool getHeight(x,y,z,...) locates the triangle that contains (x,y) and finds the height value z of the point. If (x,y) is outside the triangulation then z is not set and the method returns false.

// 6: Find the height at arbitrary (x,y) coordinates
void heightQueries()
{
	// * 1 *   Create a surface and fetch the triangles
	Fade_2D dt;
	createTriangulation(dt);

	// * 2 *   Retrieve the height values at arbitrary (x,y) coordinates
	for(int i=0;i<10;++i)
	{
		double x((100.0*rand())/RAND_MAX);
		double y((100.0*rand())/RAND_MAX);
		double z;
		bool bHaveHeight(dt.getHeight(x,y,z));
		if(bHaveHeight)
		{
			cout<<"x="<<x<<", y="<<y<<", z="<<z<<endl;
		}
		else
		{
			cout<<"x="<<x<<", y="<<y<<" is out of bounds"<<endl;
		}
	}
}


* Height Queries

x=15.6679, y=40.0944, z=27.2008

x=12.979, y=10.8809, z=15.9557

x=99.8925, y=21.8257, z=17.4128

x=51.2932, y=83.9112, z=64.6294

x=61.264, y=29.6032, z=23.9884

x=63.7552, y=52.4287, z=35.941

x=49.3583, y=97.2775 is out of bounds

x=29.2517, y=77.1358, z=52.2147

x=52.6745, y=76.9914, z=55.0812

x=40.0229, y=89.1529 is out of bounds

“The getHeight() method accepts two optional parameters: First you can use Triangle2* pApproxT to speed up the point location if you happen to know a nearby triangle. Second, use the tolerance parameter to calculate a height even if the query-point is slightly out of bounds, as it can happen due to rounding errors.”

Leave a Reply

Your email address will not be published.