Triangle Filtering: A Practical Solution in Land Survey Software

If you’re a software developer in land surveying, you understand the importance of processing large point clouds efficiently. You also know the critical role of triangle filtering to generate correct terrain representations. Automatically removing unwanted triangles while retaining the important ones is a crucial step in achieving this goal.

In this article, we’ll explore a real-world example in C++ of how to use the powerful Fade2D Delaunay triangulation SDK to remove unwanted triangles. We’ll guide you through the process of simplifying and triangulating a point cloud. We’ll also show you how to auto-filter out the triangles you don’t need and analyze connected components. This will help you keep only the terrain representations that matter for your work.

You can find the source code for this example within the downloadable Fade2D Library package, located in the ‘examples_real/removeUnwantedTriangles/‘ directory. This allows you to see it in action and apply it to your projects.

Join us in exploring the removal of unwanted triangles and its impact on the resulting terrain.

Loading the point cloud

The initial step of our processing pipeline involves loading the point cloud data. You can provide the points over the API or load them; in the simplest case from an ASCII file containing just ‘x y z’ coordinates. In this example, we will load the point cloud from a binary file. Alternatively, it’s worth noting that you can also import an existing triangulation.

// * Step 1 *   Load the point cloud 
vector<Point2> vOrgPoints;
readPointsBIN("point_cloud.bin",vOrgPoints,true);
size_t orgSize(vOrgPoints.size());
cout<<"Original number of points: "<<orgSize<<endl;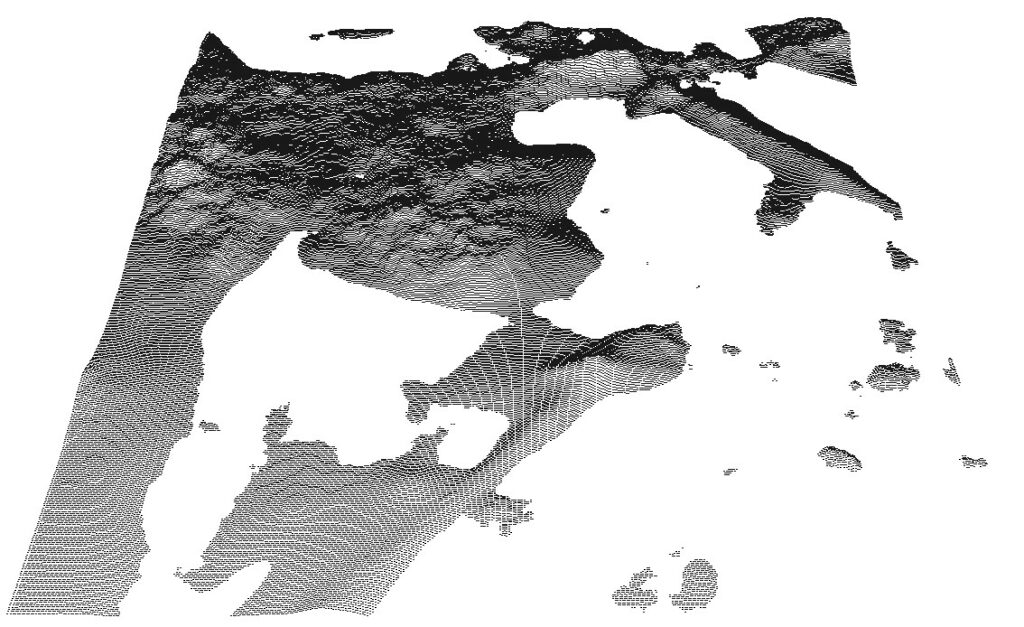

Reducing the point cloud size

To proceed, we will now reduce the size of the point cloud. There are multiple techniques to accomplish this. One such approach is adaptive simplification which preserves more points in areas with significant changes and removes more in flat regions that are of less interest. Another method involves using a grid to cluster the points. From each cluster, we can choose to retain the lowest point, the highest point, an average point, or the point whose height corresponds to the median height of the cluster.

// * Step 2 *   Reduce the cloud size
CloudPrepare cloudPrep;
cloudPrep.add(vOrgPoints);
vOrgPoints.clear(); // In order to save memory!
double maxDiffZ(1.0); // maximum z-tolerance per point cluster
SumStrategy sumStrategy(SMS_MINIMUM); // SMS_MINIMUM serves ground filtering
ConvexHullStrategy chStrategy(CHS_MINHULL); // CHS_NOHULL or CHS_MAXHULL or CHS_MINHULL
size_t approxNumPoints(0.3*orgSize); // The desired (approx.) number of output points
cloudPrep.uniformSimplifyNum(approxNumPoints,sumStrategy,chStrategy);
cout<<"Reduced number of points: "<<cloudPrep.getNumPoints()<<endl;

In our current scenario, we’ve opted for a grid-based approach to shrink the point cloud size to one-third. We’ve chosen the lowest point from each cluster, which corresponds to ground-filtering, removing higher points that probably represent vegetation and retaining those that rather indicate the ground.

Triangulating the point cloud

Now that we have reduced the point cloud, we can proceed to triangulate it i.e., to create a mesh of triangles.

// * Step 3 *   Triangulate the reduced point cloud
Fade_2D dt;
dt.insert(&cloudPrep,true);

However, a Delaunay triangulation is always convex and thus the created mesh includes undesirable triangles, such as those with very long edges or near-vertical angles. Removing these unwanted triangles will be the focus of our next steps.

The peelOffIf() function

To remove unwanted triangles from the mesh, we will use Fade2D’s peelOffIf() function, which eliminates bad triangles from the border of a triangulation. This is an iterative process i.e., when border triangles are removed then inner triangles may become new border triangles which may later also be removed and so on. This process continues until there are no more bad triangles on the mesh border..

The peelOffIf() function does NOT remove triangles from the triangulation. Instead, it returns a new zone that contains only the retained triangles. If peelOffIf() should not keep any triangle, then it returns a NULL pointer rather than an empty zone, so make sure to check this case!

What criteria determine if a triangle is considered “bad”? These rules are customizable, and the user can define them by implementing a custom predicate as explained in the following section.

First Triangle Filtering Stage

double medianLen(getLengthPercentile(dt,0.5));
Zone2* pGlobalZone(dt.createZone(NULL,ZL_GLOBAL));
PeelDeciderAggressive aggressiveDecider(3*medianLen);
Zone2* pFiltered1=peelOffIf(pGlobalZone,true,&aggressiveDecider); // bAvoidSplit=true

The code snippet above first computes the median of the edge lengths of the triangulation. Then, a user-defined PeelDeciderAggressive class, derived from PeelPredicateTS, identifies border triangles as bad based on any of three criteria:

1. an edge length exceeding a threshold (set at 3 times the median length),
2. the triangle is almost vertical, or
3. an inner angle at a vertex that is opposite a border edge and greater than 140 degrees.

While the above rules are rather aggressive, we can prevent them from subdividing connected components of the triangulation by calling the peelOffIf() function with the parameter bAvoidSplit=true.

// A customized peel predicate based on PeelPredicateTS that allows
// users to define their own criteria for removing or keeping border
// triangles.
class PeelDeciderAggressive:public PeelPredicateTS
{
public:
	PeelDeciderAggressive(double maxEdgeLen_):
		sqMaxEdgeLen(maxEdgeLen_*maxEdgeLen_)
	{}

	// This function is called from peelOffIf() with a border triangle
	// pT. It will remove pT if this function returns true.
	bool operator()(const Triangle2* pT,std::set<Triangle2*>* pCurrentSet)
	{
		// * 1 *   If one edge of pT is larger than the maximum edge
		//         length then it must be removed - return true!
		for(int i=0;i<3;++i)
		{
			double sqLen(pT->getSquaredEdgeLength25D(i));
			if(sqLen>sqMaxEdgeLen) return true; // Too large!
		}

		// * 2 *   An almost vertical border triangle must be removed.
		Vector2 nv(pT->getNormalVector()); // Normal vector
		Vector2 up(0,0,1); // Vertical vector
		double cosPhi(nv*up); // cos(angle)
		double angle;
		if(cosPhi>=-1.0 && cosPhi<=1.0)
		{
			angle=acos(cosPhi)*57.2958; // Normal case, compute the angle
		}
		else
		{
			// Robustness in case of numeric inaccuracy
			if(cosPhi>1.0) angle=0;
				else angle=180.0; // cosPhi<-1.0
		}
		if(angle>85.0)
		{
			// Triangle almost vertical - return true to remove it
			return true;
		}

		// * 3 *   Remove pT if a vertex opposite to a border edge
		//         has a very large interior angle.
		for (int i = 0; i < 3; ++i)
        {
			// Is the opposite edge of i a border edge of the zone?
			Triangle2* pNeigT(pT->getOppositeTriangle(i));
			if(	pNeigT==NULL ||
				pCurrentSet->find(pNeigT)==pCurrentSet->end() )
			{
				// Yes, border. Check the interior angle:
				if (pT->getInteriorAngle25D(i) > 140)
				{
					return true;
				}
			}
        }
        return false;
	}
	double sqMaxEdgeLen;
};

It’s worth emphasizing that the PeelDeciderAggressive class described above is a user-defined predicate. While the above example implementation works well, you have the flexibility to use entirely different criteria for your PeelDecider if desired.

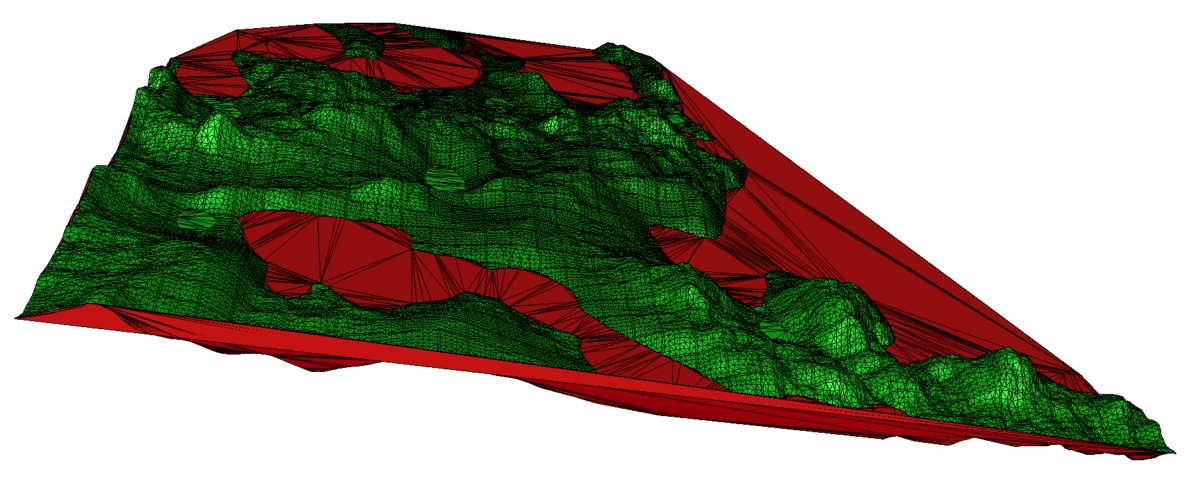
In the image above, you can see that the combination of peelOffIf() and PeelDeciderAggressive has effectively eliminated numerous undesirable triangles. Nonetheless, several unwanted triangles persist, which we will address in the subsequent filtering steps.

Second Triangle Filtering Stage

In this stage, we apply another round of filtering using peelOffIf(), this time allowing connected components to be split. However, we use a milder PeelPredicate that does not remove as many triangles as the previous aggressive one. As a result the triangulation remains intact.

// * 5 *   Filtering Stage 2: A careful peel decider applied by
//         peelOffIf decides to remove only triangles with edges
//         greater than 10 times the median edge length.
//         This time peelOffIf() may split connected components
PeelDeciderCareful carefulDecider(10*medianLen);
Zone2* pFiltered2=peelOffIf(pFiltered1,false,&carefulDecider); // bAvoidSplit=false

Here is the careful PeelPredicate we use in this stage. It contains only one simple criterion: Triangles with an edge longer than 10 times the median length are bad.

class PeelDeciderCareful:public PeelPredicateTS
{
public:
	PeelDeciderCareful(double maxEdgeLen_):sqMaxEdgeLen(maxEdgeLen_*maxEdgeLen_)
	{
	}
	bool operator()(const Triangle2* pT,std::set<Triangle2*>* )
	{
		// Edge length
		for(int i=0;i<3;++i)
		{
			double sqLen(pT->getSquaredEdgeLength25D(i));
			if(sqLen>sqMaxEdgeLen) return true; // Too large!
		}
		return false;
	}
	double sqMaxEdgeLen;
};

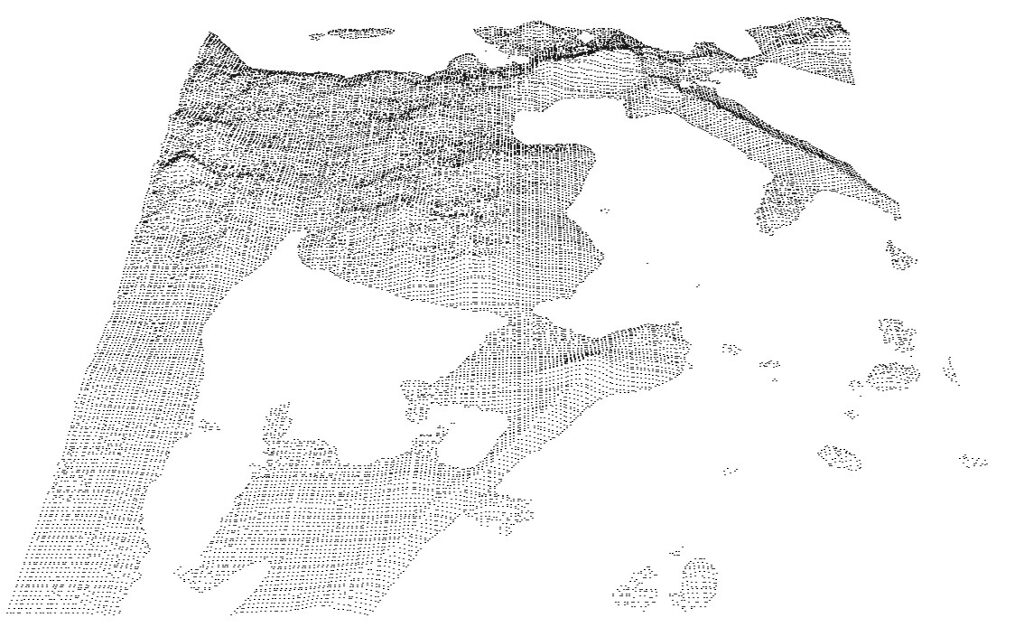
As seen in the image above, the second filtering stage has improved the triangulation further. Nonetheless, there are still a few small connected components comprised of only a few triangles. These will be eliminated in the final stage of triangle filtering below.

Removing Tiny Connected Components

The following code uses a function from Fade2D to determine the individual connected components of the remaining triangulation. It then iterates over them and removes those that consist of less than 50 triangles.

// * 6 *   Form connected components
vector<Triangle2*> vT2;
pFiltered2->getTriangles(vT2);
vector<vector<Triangle2*> > vvT;
getConnectedComponents(vT2,vvT);
cout<<"number of connected components="<<vvT.size()<<endl;

// * 7 *   Keep only large connected components 
vector<Triangle2*> vFinalT;
int numComponentsKept(0);
const double MINIMUM_NUM_T(50);
for(vector<Triangle2*>& vT:vvT)
{
	if(vT.size()>MINIMUM_NUM_T)
	{
		++numComponentsKept;
		copy(vT.begin(),vT.end(),back_inserter(vFinalT));
	}
}
cout<<"number of kept components="<<numComponentsKept<<endl;
Zone2* pFinalZone(dt.createZone(vFinalT));

cout<<"Writing final.obj"<<endl;
pFinalZone->writeObj("final.obj");
return 0;

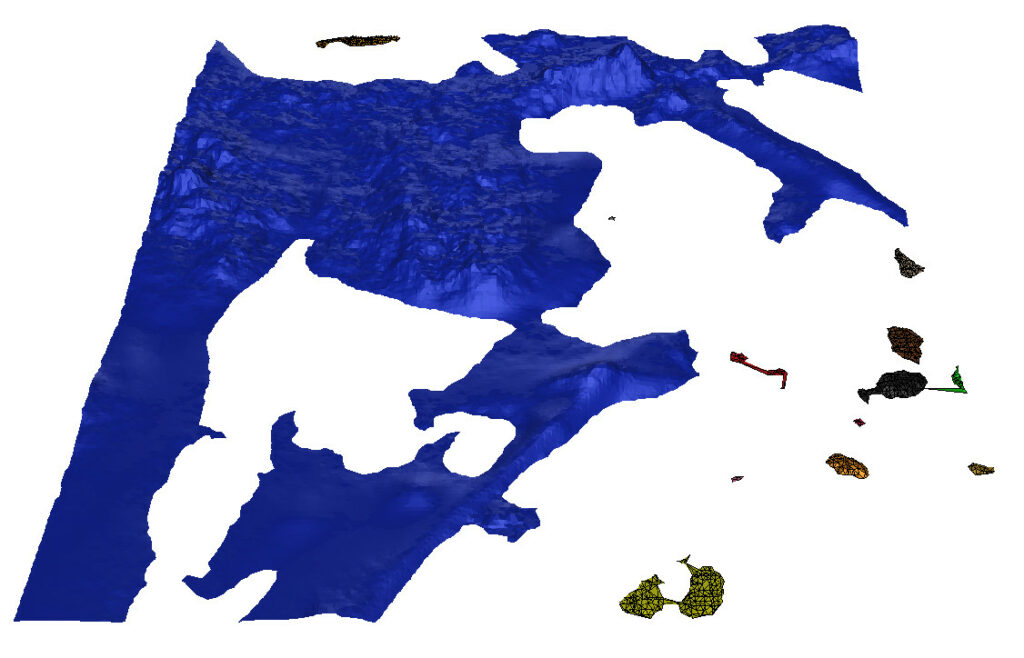
Final Result

We’ve covered the process of creating and filtering terrain triangles using the Fade2D Delaunay triangulation library. After simplifying the point cloud and removing the majority of unwanted triangles with the custom PeelDeciderAggressive, we proceeded with a second round of triangle filtering, employing a different Peel Predicate, and then eliminated tiny connected components. The resulting triangulation now exactly represents the desired data, as illustrated in the image below:

Using Fade2D can significantly simplify the process of creating a high-quality triangulation. However, it’s essential to carefully choose the filtering criteria to ensure that the resulting triangulation is suitable for your specific use case. With a little bit of experimentation and parameter tweaking, you can fine-tune the parameters to obtain the best possible result for your specific needs.

We hope that this article has provided you with valuable insights and tips on how to filter your Delaunay triangulation using the Fade2D library.