A frequently asked question is how to export a triangulation as a list of points and indices for use in one’s own software. Users have two options: they can implement this themselves, or they can utilize the FadeExport data structure. Using FadeExport is memory-efficient as it can optionally release memory within Fade while building the FadeExport data structure, thus preventing memory usage peaks during the data export.
The FadeExport Data Structure
FadeExport is a fairly simple struct with a few methods for convenient usage and also for demonstration purposes. It is intentionally implemented in a header file, allowing you to easily adapt the source code for your project.
struct FadeExport
{
void print() const;
bool writeObj(const char* filename) const;
void extractTriangleNeighborships(std::vector<std::pair<int,int> >& vNeigs) const;
void getCornerIndices(int triIdx,int& vtxIdx0,int& vtxIdx1,int& vtxIdx2) const;
void getCoordinates(int vtxIdx,double& x,double& y) const;
// DATA
double* aCoords; ///< Cartesian coordinates (dim*numPoints)
int* aCustomIndices; ///< Custom indices of the points (only when exported)
int* aTriangles; ///< 3 counterclockwise oriented vertex-indices per triangle (3*numTriangles)
};
Data Export from Fade
- Step 1 in the code below creates some points. However, the order in which we pass these points to Fade may not be the same as the order in which we receive them later. Therefore, we can optionally use
Point2::setCustomIndex()to set our own indices for the points. - Step 2 inserts the points into a Fade_2D object
- Step 3 uses
Fade_2D::exportTriangulation()to store the geometry data in aFadeExportstruct. You can specify whether you also want to export the custom indices and whether you want to release data in theFade_2Dobject bit by bit during the export. The latter is particularly useful for handling large data, because it prevents temporary data duplication in memory until the Fade_2D object can be deleted.
// * 1 * Create some points
std::vector<Point2> vPoints;
generateCircle(6,25.0,25.0,10.0,10.0,vPoints);
for(size_t i=0;i<vPoints.size();++i)
{
// Optional: Set an arbitrary custom index
vPoints[i].setCustomIndex(int(i));
}
// * 2 * Triangulate
Fade_2D dt;
dt.insert(vPoints);
// * 3 * Export (clears the Fade object)
FadeExport fadeExport;
bool bCustomIndices(true); // To retrieve custom indices also
bool bClear(true); // Clear memory in $dt
dt.exportTriangulation(fadeExport,bCustomIndices,bClear);
//////////////////////////////////////////////////////
// The Fade object has been cleared to avoid memory //
// peaks. Now verify if we have received all data...//
//////////////////////////////////////////////////////
...For demonstration purposes, i.e., to show you how to access the exported information, the code in Steps 4, 5, and 6 prints and draws the data in the FadeExport struct.
- Step 4: We iterate over the vertex indices and retrieve the
x,ycoordinates (orx,y,zin the 2.5D case). These coordinates are stored inFadeExport::aCoordsand you can access them either through indices or conveniently via thegetCoordinates(vtxIdx,x,y)method. - Step 5: We output the triangles and draw them. To achieve this we determine the three vertex indices per triangle index and, for each vertex-index, we retrieve the associated coordinates. Although we could calculate the indices and access the arrays directly, using the
getCornerIndices()andgetCoordinates()methods is a more convenient and user-friendly approach. - Step 6: Fade does not explicitly store information about which triangle is adjacent to another to conserve additional memory in the FadeExport struct. If your data structure requires this information, you can rapidly determine it from the other stored data using the
extractTriangleNeighborships()method.
...
//////////////////////////////////////////////////////
// The Fade object has been cleared to avoid memory //
// peaks. Now verify if we have received all data...//
//////////////////////////////////////////////////////
// * 4 * Vertex output
Visualizer2 visExp("example8_exported.ps");
for(int vtxIdx=0;vtxIdx<fadeExport.numPoints;++vtxIdx)
{
double x,y;
fadeExport.getCoordinates(vtxIdx,x,y);
std::string s(" "+toString(vtxIdx));
// Are there custom indices? Then add
if(fadeExport.numCustomIndices==fadeExport.numPoints)
{
int customIdx(fadeExport.aCustomIndices[vtxIdx]);
s.append("(customIdx="+toString(customIdx)+")");
}
std::cout<<"Vertex"<<s<<": "<<x<<" "<<y<<std::endl;
Label label(Point2(x,y),s.c_str(),true,15);
visExp.addObject(label,Color(CRED));
}
// * 5 * Triangle output
for(int triIdx=0;triIdx<fadeExport.numTriangles;++triIdx)
{
int vtxIdx0,vtxIdx1,vtxIdx2;
fadeExport.getCornerIndices(triIdx,vtxIdx0,vtxIdx1,vtxIdx2);
std::cout<<"Triangle "<<triIdx<<": "<<vtxIdx0<<" "<<vtxIdx1<<" "<<vtxIdx2<<std::endl;
// Fetch also the coordinates and draw the edges
double x0,y0;
double x1,y1;
double x2,y2;
fadeExport.getCoordinates(vtxIdx0,x0,y0);
fadeExport.getCoordinates(vtxIdx1,x1,y1);
fadeExport.getCoordinates(vtxIdx2,x2,y2);
Point2 p0(x0,y0);
Point2 p1(x1,y1);
Point2 p2(x2,y2);
visExp.addObject(Segment2(p0,p1),Color(CBLACK));
visExp.addObject(Segment2(p1,p2),Color(CBLACK));
visExp.addObject(Segment2(p2,p0),Color(CBLACK));
double midX((x0+x1+x2)/3.0);
double midY((y0+y1+y2)/3.0);
std::string text("T"+toString(triIdx));
Label l(Point2(midX,midY),text.c_str(),true,15);
visExp.addObject(l,Color(CBLUE));
}
// * 6 * Neighbors output
std::vector<std::pair<int,int> > vNeigs;
fadeExport.extractTriangleNeighborships(vNeigs);
for(size_t i=0;i<vNeigs.size();++i)
{
std::cout<<"Triangle "<<vNeigs[i].first<<" <-> Triangle "<<vNeigs[i].second<<std::endl;
}
visExp.writeFile(); // Write the postscript file
// The above is for demonstration purposes, the easier way
// to output FadeExport data is using its print() or writeObj()
// function:
//fadeExport.print();
//fadeExport.writeObj("out.obj");
return 0;The output of Example 8 is:
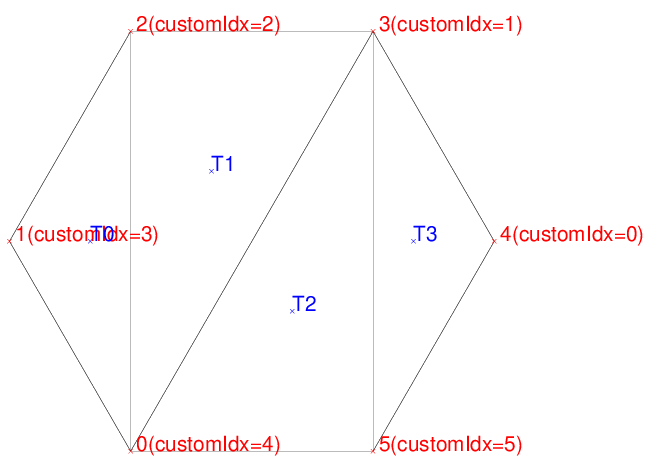
Vertex 0(customIdx=4): 20 16.3398
Vertex 1(customIdx=3): 15 25
Vertex 2(customIdx=2): 20 33.6603
Vertex 3(customIdx=1): 30 33.6602
Vertex 4(customIdx=0): 35 25
Vertex 5(customIdx=5): 30 16.3397
Triangle 0: 0 2 1
Triangle 1: 3 2 0
Triangle 2: 5 3 0
Triangle 3: 5 4 3
Triangle 0 <-> Triangle 1
Triangle 1 <-> Triangle 2
Triangle 2 <-> Triangle 3
4 replies on “Exporting a Triangulation – Example 8”
Has the custom indices option any drawback like decreased performance?
No. The index field belongs to the point class anyway and exporting them is fast, you will not notice any difference.
Hi!
We are doing some research on distributed quality meshing and would like to be able to receive zones from other nodes and insert them into the local Fade_2D object. Does Fade_2D::load allow for that or does it only support loading zones into an empty Fade_2D object? If it’s the latter, are there other ways to combine two triangulations or zones (I’m not sure if this matters but the two triangulations or zones we’ll be combining are adjacent in the original mesh.) Put simply, We’re hoping to effectively slice a mesh in half, optimize each half separately, and stitch it back together.
Thanks in advance!
Hi!
Fade_2D::load() loads into an empty object. But combining two quality meshes where all triangles are Delaunay, i.e., if there are no vertices in the circumcircle of each triangle, is easy: Simply insert the vertices of one triangulation into the other triangulation. If this does not suffice, insert constraint edges to establish exactly the same triangles in the target triangulation.
Besides, when implementing this kind of stuff, it may be helpful to be aware of the following nasty property: If you split a line segment (p0,p1) in the middle, then floating point arithmetic does not guarantee that (p0,splitPoint,p1) are collinear. This is not only due to inaccurate computation: There are settings where you can’t find even a single point in floating point coordinates that is exactly ON the line (p0,p1)