2.5D Terrain Triangulation and Point Cloud Simplification

2.5D Delaunay triangulations (TIN – Triangulated Irregular Networks) are like a 2D Delaunay triangulation, but with elevated points. This article first describes the simple triangulation of point clouds from LiDAR scans and surface metrology data. It then demonstrates their optional simplification using adaptive and grid-based clustering methods. Finally, it shows how to re-export the triangle-mesh to your own data structures.

For clarity, this example consists of the Sub-Examples 0-4, each comprising only a few lines of code. You can find the C++ source code as part of the Fade download in the file “examples_25D/a_terrain25d.cpp“.

Generating Points

The function getInputPoints() in the example source code takes a filename and returns a vector of points.

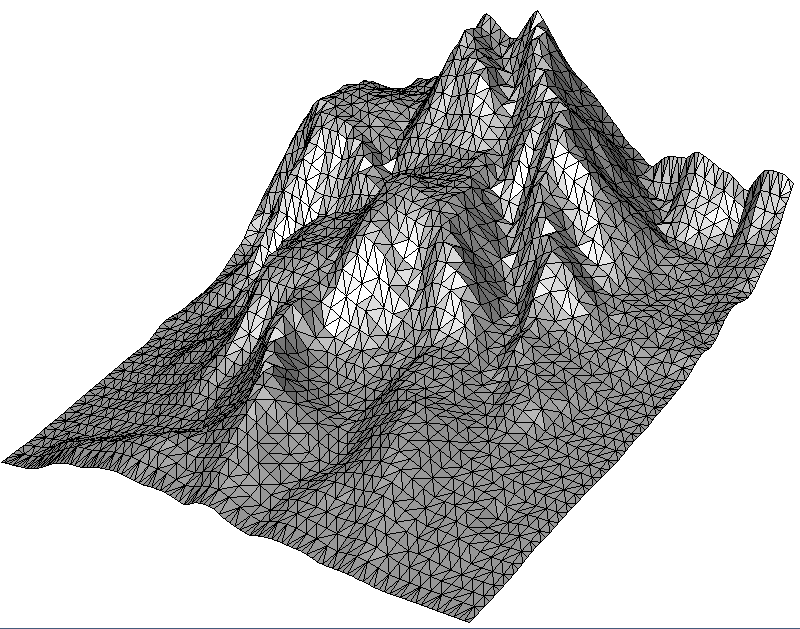
• The special filename “MOUNTAIN” yields a small predefined demo point-cloud with 9240 points (105×88)
• An empty filename yields a random 2.5D surface point cloud. To learn more, see generateRandomSurfacePoints()in the module Test Data Generators.
• Any other filename names a “x y z”-ASCII file. You can substitute the name of your own file here. See readXYZ() in the module File I/O where various read/write functions for ASCII and binary files are documented.

void getInputPoints(const std::string& filename,
					std::vector<Point2>& vPointsOut)
{
	if(filename=="MOUNTAIN")
	{
		getMountain(vPointsOut);
	}
	else if(!filename.empty())
	{
		// Read terrain points from an ASCII file
		readXYZ(filename.c_str(),vPointsOut);
	}
	else
	{
		// No file given, create a random surface for the demo
		generateRandomSurfacePoints(
			100, // numPointsX
			100, // numPointsY
			200, // numCenters (waviness)
			0,0,0,100,100,50, // Bounds xmin,ymin,zmin,xmax,ymax,zmax
			vPointsOut, // Output vector
			1  // Seed (0 is random, >0 is static)
			);
	}
	std::cout<<"Original number of points: "<<vPointsOut.size()<<endl;
}

2.5D Delaunay Triangulation

The code snippet below represents Sub-Example 0. Its Step1 uses the getInputPoints()function described above to fetch points. Then Step2 makes performance settings, creates a CloudPrepare object, adds the points to it and finally inserts the CloudPrepare object into the 2.5D Delaunay triangulation. Finally, Step3 saves the result as a .vtk file that can be viewed with Paraview. Alternative file formats are .obj file (supported by practically any 3D viewer) and .list for Geomview (Linux).

// 0: Triangulate all points
void terrain_full()
{
	// * Step 1 *   Get input points
	std::vector<Point2> vInputPoints;
	getInputPoints("MOUNTAIN",vInputPoints);

	// * Step 2 *   Triangulate
	Fade_2D dt;
	dt.setFastMode(true); // Fast mode greatly accelerates raster points
    dt.setNumCPU(0); // 0 means: autodetect
	// dt.insert(vInputPoints); // Still possible but CloudPrepare is recommended
	CloudPrepare cloudPrep;
	cloudPrep.add(vInputPoints);
	dt.insert(&cloudPrep,true); // More memory efficient

	// * Step 3 *   Show
	write(0,"terrain_full",dt);
}

“You could also insert the vector with the points directly in Fade_2D. However, doing it via the CloudPrepare object has a practical advantage: Since adding the points to CloudPrepare and inserting the CloudPrepare object into the Delaunay triangulation are two individual steps, you have the opportunity to delete the points from the data structures of your own software in an intermediate step i.e., before any additional memory for triangles is reserved by Fade. Otherwise, the points would reside twice in memory for a short time. This avoids memory consumption peaks.”

“The code above makes two performance settings:

1. Fade_2D::setFastMode(true) enables a triangulation mode that accelerates triangulation of raster data (points on a regular grid).

2. By default Fade runs single-threaded. But you can enable more cores with Fade_2D::setNumCPU(0). Thereby the special value 0 means autodetect.”

Reducing a Point Cloud

Preventing memory consumption peaks is just one purpose of the CloudPrepare class. Moreover you can use it also to simplify point clouds using one of the below three methods:

• Sub-Example 1 demonstrates adaptive point cloud simplification by clustering points with similar height values. Geometrically, this method gives the best results because it removes the less needed vertices.
• Sub-Example 2 shows uniform simplification by a grid, where the user specifies the cell size. The algorithm summarizes all points within a grid cell.
• Sub-Example 3 reduces the point cloud also with a grid, but determines the grid size itself to match the desired number of output points specified by the user.

// 1: Simplify: Adaptive, cluster points based on their height difference
void terrain_adaptiveSimplify()
{
  	...
 	// * 3 *   Reduce the cloud size
	double maxDiffZ(1.0); // z-tolerance per point group
	SumStrategy sms(SMS_AVERAGE); // or SMS_MEDIAN, SMS_MINIMUM, SMS_MAXIMUM
	ConvexHullStrategy chs(CHS_MAXHULL); // or CHS_NONE, CHS_MINHULL
	cloudPrep.adaptiveSimplify(maxDiffZ,sms,chs,false); // bDryRun=false
	...
}

// 2: Simplify: Use a grid to cluster points
void terrain_gridSimplify()
{
	...
  	// * 3 *   Reduce the cloud size
	SumStrategy sms(SMS_AVERAGE); // or SMS_MEDIAN, SMS_MINIMUM, SMS_MAXIMUM
	ConvexHullStrategy chs(CHS_MAXHULL); // or CHS_NONE, CHS_MINHULL
	double gridLength(2);
	cloudPrep.uniformSimplifyGrid(gridLength,sms,chs,false); // bDryRun=false
	...
}

// 3: Simplify: Use approxNumPoints to cluster points (also grid-based)
void terrain_numPointsSimplify()
{
	...
  	// * 3 *   Reduce the cloud size
	SumStrategy sms(SMS_AVERAGE); // or SMS_MEDIAN, SMS_MINIMUM, SMS_MAXIMUM
	ConvexHullStrategy chs(CHS_MAXHULL); // or CHS_NONE, CHS_MINHULL
	double approxNumPoints(vInputPoints.size()/4);
	cloudPrep.uniformSimplifyNum(approxNumPoints,sms,chs);
	...
}

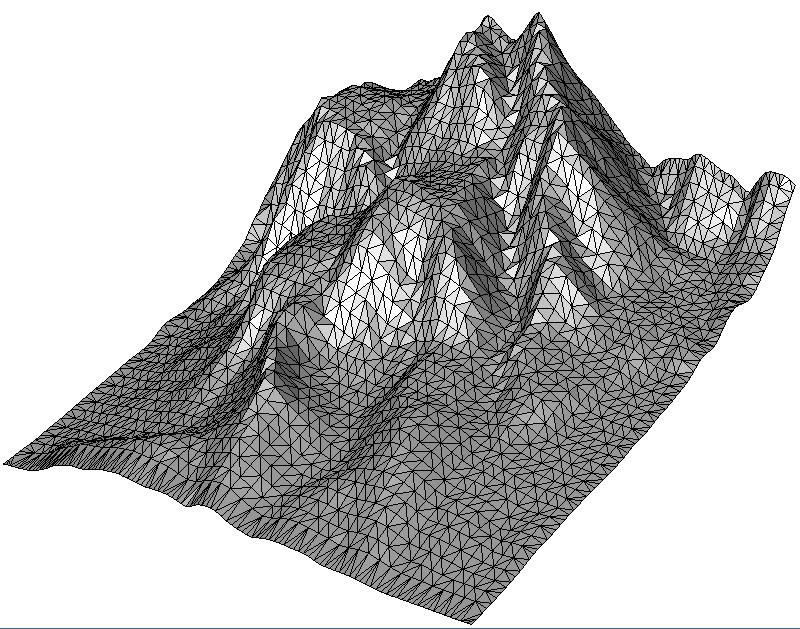
Two parameters in the above code need an explanation:

• The SumStrategy determines how points in a group are summarized. Most of the time SMS_AVERAGE will give good results. If the data contains outliers, SMS_MEDIAN is more stable. Simple ground filtering can be achieved with SMS_MINIMUM, since selecting the lowest point in the cluster ignores those higher points corresponding to vegetation. SMS_MAXIMUM is also available.
• The ConvexHullStrategy determines whether and which points of the convex hull must be left unchanged. The value CHS_NONE ignores the convex hull and simply treats all points the same. CHS_MAXHULL protects all points of the convex hull i.e., it keeps them constant, CHS_MINHULL protects only those points of the convex hull whose absence would change the shape of the convex hull. That is, it does not protect points that lie in the middle of a convex-hull line segment.
• The commands return the resulting size of the point cloud. To determine the size in advance without actually simplifying the point cloud, the parameter bDryRun can be set to true.

Exporting the final Triangulation

You probably want to have your 2.5D Delaunay triangulation not only in the Fade library, but also bring it back into your own software. This must be quick, convenient and without the triangle mesh residing in memory twice at any point. There is now a ready-made solution for triangulation-export in Fade and the earlier Example 8 describes it already for the 2D case. But for self-containedness we treat this export-solution also with the present 2.5D terrain example: We use a simple struct to store all triangulation data:

“Note: Alternatively you can also save a Delaunay triangulation to a file and reload it later”

struct FadeExport
{
 void print() const;
 bool writeObj(const char* filename) const;
 void extractTriangleNeighborships(std::vector<std::pair<int,int> >& vNeigs) const;
 void getCornerIndices(int triIdx,int& vtxIdx0,int& vtxIdx1,int& vtxIdx2) const;
 void getCoordinates(int vtxIdx,double& x,double& y) const;

 // DATA
 double* aCoords; ///< Cartesian coordinates (dim*numPoints)
 int* aCustomIndices; ///< Custom indices of the points (only when exported)
 int* aTriangles; ///< 3 counterclockwise oriented vertex-indices per triangle (3*numTriangles)
};

// 4: Export data of the triangulation
void exportData()
{
	...
	Fade_2D dt;
	dt.insert(&cloudPrep,true);

	// * 3 *   Export to a struct
	FadeExport fadeExport; // Simple struct, see "FadeExport.h"
	bool bCustomIndices(true); // To retrieve custom indices also
	bool bClear(true); // Clear memory in dt to save memory
	dt.exportTriangulation(fadeExport,bCustomIndices,bClear);

	// All triangulation data is in 'fadeExport' now and dt has
	// been cleared during the export procedure to avoid memory
	// usage peaks: dt is empty now.

	// * 4 *   Show that all data is in fadeExport
	fadeExport.print();
	fadeExport.writeObj("exportTest25D.obj");

	// NOTE: You have full access to the data in the FadeExport struct
	// and you have also access to the source code because it has been
	// implemented only in the header file "FadeExport.h". Adapt it
	// to your needs. Have also a look at the similar example in the
	// examples_2D folder.	
}